Objectifs globaux

1. Comprendre le fonctionnement d'une classification ;
2. Mettre en place des algorithmes de classification.

Activité 2 - Algorithmes KNN

Définition

KNN signifie K near-neighbors, soit les K plus proches voisins.
Un algorithme KNN est un algorithme dit de classification, permettant de déterminer l'appartenance d'une donnée à un groupe, suivant ses K plus proches voisins.

TP

Le TP est découpé en 2 parties :

• Visualiser des données pour déterminer graphiquement l'appartenance ;
• Créer un algorithme qui déterminera pour nous une valeur d'appartenance.

Visualiser un jeu de données

Objectif

À partir d'informations stockées dans un fichier csv, nous allons programmer un graphe en nuage de points, pour déterminer graphiquement des futures valeurs.

Jeu de données

Un jeu de données est une collection de données, accessibles, et structurées.
Les données sont réparties en un ensemble d'attributs, permettant d'obtenir plusieurs informations sur une donnée.

CSV

Les jeux de données sont souvent stockés dans des fichiers au format csv (Commat Separate Value) ; c'est un type de fichier où les données enregistrées sont séparées par des points virgule.
Avec ce type de fichier, nous pouvons très facilement récupérer des informations pour les manipuler.

1. Télécharger le fichier CSV reussite_exam.csv.
2. Ouvrir ce fichier sur excel pour visualiser les informations stockées.

Sur la première ligne, on peut voir quelles sont les informations, séparées par des virgules.

3. Repérer leur nom et les noter quelque part, elles serviront plus tard.

Contexte

Le document indique la réussite ou l'échec d'un élève à un devoir, suivant son temps de révision, et sa précédente note (notée sur 100).

Bibliothèques à utiliser

Pour manipuler ce fichier sur python, nous allons utiliser 2 bibliothèques différentes :

• pandas pour importer des fichiers csv;
• matplotlib pour dessiner des graphes.

Pour matplotlib, il faudra écrire cette ligne :

import matplotlib.pyplot as plt

On importe la fonctionnalité pyplot de matplotlib, et on renomme le tout en plt (pour éviter d'avoir à écrire "pyplot" partout).
Pour utiliser les différentes fonctions de pyplot, il faudra écrire plt.fonction(), où fonction() représente une des fonctions à utiliser.

4. Importer les bibliothèques pands et pyplot de matplotlib.

pandas possède une fonction appelée read_csv(fichier), qui ouvre un fichier CSV, et le retourne.

5. Utiliser cette fonction, et stocker dans une variable exam le fichier ouvert.

Nous allons maintenant séparer les 3 informations du document en 3 listes différentes :

• liste_heure : représentant les valeurs de l'abscisse du graphe ;
• liste_score : représentant les valeurs de l'ordonnée du graphe ;
• liste_reussite : indiquant l'appartenance au groupe échec ou réussite des points du graphe.

On donne la ligne de code suivante :

liste_heure = exam.loc[:,"Heure_etude"].values

Qui permet de stocker dans la variable liste_heure l'ensemble des informations de la colonne "Heure_etude" du fichier csv.

6. En utilisant l'exemple de cette ligne, rajouter 2 lignes permettant de stocker les listes des 2 dernières informations.

On dispose des fonctions suivantes :

Rajout de points

scatter(x,y,color='',label='')

Rajoute les points de la liste x et y, avec une couleur de point, et la légende associée au point :

• x : listes des abscisses ;
• y : liste des ordonnées ;
• color='' : couleur à préciser (str) ;
• label='' : légende du point (str).

Légende abscisse

xlabel(legende)

Donne une légende à l'axe x (str).

Légende ordonnée

ylabel(legende)

Donne une légende à l'axe y (str).

Titre du graphe

title(titre)

Donne un titre au graphe (str).

Générer le graphe

legend()

Génère le graphe suivant les fonctions précédentes.

Montrer le graphe

show()

Affiche le graphe généré.

7. À l'aide des fonctions du tableau, écrire les instructions permettant d'afficher un graphe dont l'abscisse correspond au nombre d'heures, et l'ordonnée au score. On pourra donner une légende aux axes x et y, et un titre au graphe.

Visuel

Si tout est bien écrit, python devrait générer ceci : 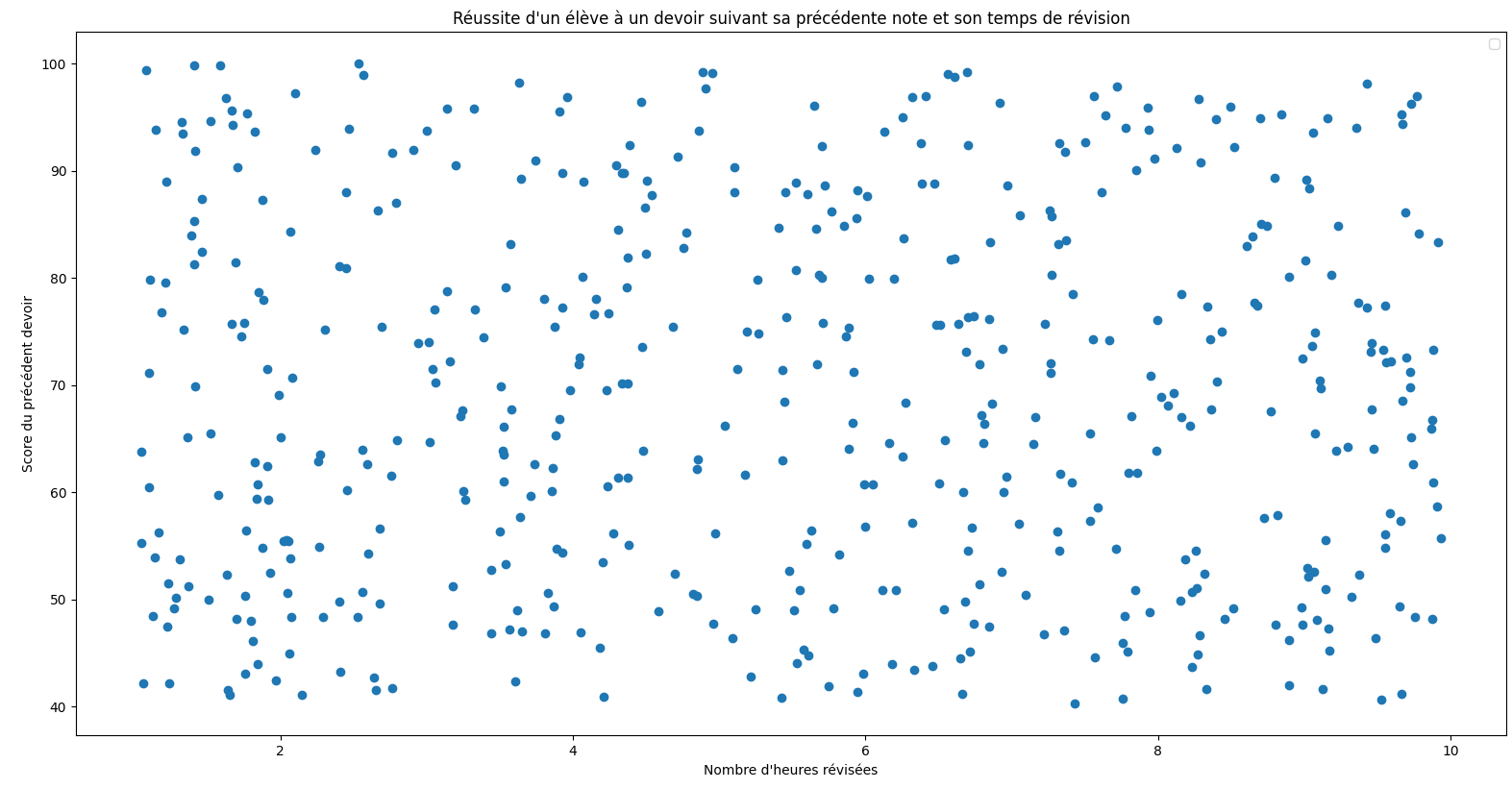Chaque point est un élève, correspondant à son nombre d'heures révisées pour un devoir, et son score à son précédent devoir.

Problème

Avec ce graphe, on ne distingue pas qui a réussi ou non le devoir.
Il va falloir utiliser la 3ème liste pour faire 2 types de points différents :

• Des points rouges, correspondant à un élève qui a échoué;
• Des points verts, correspondant à un élève qui a réussi.

La fonction scatter permettant l'affichage de tous les points, il faut lui préciser de ne prendre que des points d'une liste répondant à un critère donné.
Pour choisir des points en fonction d'un critère, on peut utiliser l'instruction : [liste_groupe == critere] sur une liste de points. Cela signifie que sur une liste donnée, on ne va prendre que des points dont les points de la liste des groupes répondent au critère donné.

8. Modifier votre code, pour que le graphe n'affiche que les points correspondant aux élèves ayant échoués. On mettra ces points en rouge, ainsi que le label échec.
9. En prenant exemple sur la ligne de code précédente, rajouter la ligne permettant d'afficher les points des élèves qui ont réussi. On les affichera en vert avec le label réussi.

Algorithme du KNN

Objectif

On souhaite vérifier si un élève va réussir ou non son devoir, suivant son temps de révisions, et la note de son dernier devoir.
Le KNN nous permettra de tenter de deviner sa réussite ou non grâce aux données déjà présentes (donc avec des profils d'élèves similaires).

1. Rajouter un point sur le graphe grâce à la fonction scatter, avec les coordonnées que vous voulez. On mettra la couleur "k", correspondant à une couleur visuelle sur le graphe pour déterminer la position du point.
2. Déterminer graphiquement si, avec les valeurs saisies, l'élève va réussir ou échouer au devoir.

Algorithme du KNN

Ce dont on a besoin pour faire l'algorithme du KNN :

• data : Un jeu de données sous la forme d'une liste ou dictionnaire;
• c : Une donnée dont on souhaite trouver le type;
• Savoir calculer une distance entre 2 points;
• k : Un entier représentant le nombre de voisins que l'on souhaite prendre.

Voici l'algorithme du KNN :

• On calcule les distances entre c , et toutes les données de data;
• On prend les k points les plus proches;
• On détermine le type de c en fonction du type apparaissant le plus parmi les points.

Distance

Il existe plusieurs formules pour calculer des distances entre 2 points. Chaque point (d1, d2) est représenté par leurs coordonnées (x1,y1) et (x2,y2) respectivement. On dispose des formules suivantes :

• Distance euclidienne : $\sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$
• Distance de Manhattan : $|x_2 - x_1| + |y_2 - y_1|$
• Distance de Tchebychev : $\max\left( |x_2 - x_1|, |y_2 - y_1| \right)$

3. Écrire une fonction distance(point1, point2), qui retourne la distance entre ces 2 points, suivant l'une des méthodes proposées.

Liste de distances

4. Écrire une fonction liste_distances(data, c), qui prend en paramètres le jeu de données data et un point c, et retourne une liste comprenant la distance entre chaque points de data, et c.

KNN

5. Écrire une KNN(data, c, k), qui retourne le type de c en prenant les k points les plus proches.

Tests

L'algorithme écrit, il faut maintenant le tester.

6. Prendre le point défini à la question 1 et un k = 3, et déterminer son type. Comparer le résultat obtenu avec celui de la question 2.
7. Mettre k = 5, et comparer à nouveau avec ce qui a été trouvé précédemment.
8. Ajouter les éléments de c dans la matrice data, ainsi que dans les listes heure, score, et reussite (en renseignant la valeur de réussite).